

The images you see spinning and morphing between shapes are animated GIF
images created by me, Albert Hines. They are built using image/video
capability on Silicon Graphics workstations. I've made them specifically to
simulate the various habits exhibited by minerals.
|
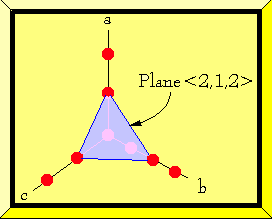
The diagram at left shows very briefly how the system works. The a, b, and c
lines show rows of molecules. The blue plane represents a crystal face. The
index tells which molecules lie on the crystal face plane by taking the
reciprocal of the intersection of the crystal plane with the axis.
|
The image below represents the forms possible as a cubic crystal takes on a
more and more octahedral habit, common in fluorite, galena, and other
isometric minerals. The faces of the cube, in terms of their Miller index,
are:
<1,0,0>,<0,1,0>,<0,0,1>,<-1,0,0>,<0,-1,0>,<0,0,-1>

where the minus corresponds to a barred, or negative, value. Since in the
isometric system, lattice axes are all mutually orthogonal and the scales
are equal, the indices are x,y,z intercepts of a plane defining the face,
e.g. <1,1,1> indicates a plane with three points: (1,0,0),(0,1,0),(0,0,1).
The <1,0,0> face, then, is defined by a plane intersecting the "a" axis
at 1, but that does not intersect either the b, or c axes (i.e. it intersects
at 1/0 or infinity). Hence, the value of
0 indicates a plane parallel to this index.
Likewise, the octahedral faces have eight Miller indices:
<1,1,1>, <-1,1,1>, <1,-1,1>, <-1,-1,1>,
<1,1,-1>, <-1,1,-1>, <1,-1,-1>, <-1,-1,-1>
which means, for example, that the first face is defined by a plane passing
through the intercept points a= 1, b=1, c=1.
Here is fluorite, above left, and galena, above right. The fluorite octahedron
from Hardin County, Illinois, is a cleavage. That is, it's actually from a
cubic crystal, but split along the <1,1,1> planes, where the ionic bond
between the calcium and the fluorine is weakest. Fluorite is often purely
octahedral, as shown in the pink specimen from Mont Blanc, Switzerland below.
The galena is from Nadan, Bulgaria and is naturally cubo-octahedral.

To accomplish all this in the virtual world, I first create a simple cube
representing a solid bounded by a = 1 & -1, b = 1 & -1, c = 1 & -1. Then I
define cutting planes passing through the octahedral faces defined by the
x,y,z coordinates stated above. These, when used to trim off the solid
extending beyond the cutting plane, form an octahedron. By then
progressively increasing or reducing the size of the cube, retaining the
cutting planes, a partially cut, i.e, cubo-octahedral, shape is produced.
By shading the image and assembling the sequential pictures, the animation
emerges!
Thus, the yellow image below portrays a cube with dodecahedral modifications.
These are accomplished with faces growing along the following 12 planes:
<1,1,0>,<1,0,1>,<0,1,1>, and all permutations with barred 1's. A
<1,1,0> faces, for example would pass through the plane containing the points:
(1,0,0),(0,1,0), and parallel to the z axis.

Below is a nice native copper with sharp dodecahedral form.
Many other minerals also commonly display this habit(
lazurite for example).

Once again using fluorite as an example, a Spanish fluorite on quartz (from
Ribadesella) below illustrates dodecahedral modifications to a cubic habit.

Trapezohedra are formed by the <2,1,1> faces, i.e. a plane passing through
the points (1,0,0), (0,2,0) and (0,0,2). They seem to be named after the
incorrect notion that the faces are trapezoidal! Trapezohedral habit is shown
beautifully below with a grossular from the Kola Peninsula (size is 17 mm).
Note the small <110> face (front & center).


Pyritohedra, and its namesake (faces are on planes <0,1,2>) are shown below.
Specimen at left is from Logrono, Spain. The pyrite at right is a sharp 4
cm. example from the island of Elba, Italy.



This pyrite from Peru shows vividly the pyritohedral modification to the basic cube. Each corner is also modified with a <1,1,1> or octahedral face.

The trisoctahedron (below)
has the Miller indices <2,2,1> and appears to be named after the fact that
it looks kind of like an octohedron, but has 3 times as many faces!

I don't have any mineral specimens clearly showing trisoctahedral habit.
All donations would be delightfully accepted!
Tetragonal or orthorhombic lattices may be fairly easily rendered by scaling
the aforementioned isometric procedure along the x, y, or z directions by
the appropriate ratios.
Other systems are not so simple. For example, the hexagonal system has
in Miller's system 4 axes: one vertical and three at 60° angles one
to another. In reality, only three of these axes are necessary. The fourth is
added only for convenience, as knowing three automatically specifies the
fourth. However, it works the same way. For example, the benitoite crystal
shown below has a small triangular "c" face along the basal pinacoid,
<1,0,0,0>. It is, therefore perpendicular to the longitudinal (spinning)
axis.
The small slanting face, known as a "p" face, has an index <1,0,1,1>. Thus,
assuming an x axis parallel to the "a" index, a y axis bisecting the "c"
and "d" indices, converting to x,y,z coordinates gives a plane passing through
the points,
(1.0 , 0.0 , 0.0), (0.0 , 0.866 , 0.5), (0.0 , 0.866 , -0.5)
This yields a crystal like that below. The real specimen is from San Benito
County, California and is one of my favorites.


Unfortunately, I have not been able to obtain realistic looking transparent
images of crystals. Rather than show crummy looking clear ones, I have opted
to render them as opaque. Sorry! Maybe I can get them some day.
Well, enough fun for today. Thanks for stopping in and have a really
magnificent day!
If you would like to take these images for your personal use, please
feel free, so long as you give proper credit (like a link to this page).
If you would like to take these images for commercial use, please ask
permission as I do charge a very reasonable fee for this. Thanks.
Return to Albert's Mineral Home Page.


















