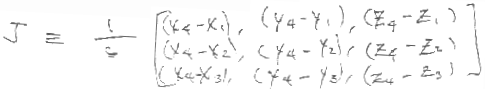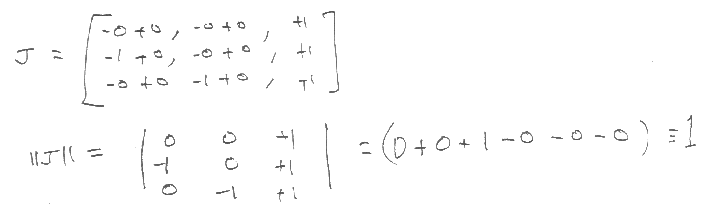Formulation of the Finite Element Jacobians

Quickly, I want to present the total details of calculating a finite element jacobian. The only important difference in this and a "REAL" jacobian is that you would need to replace the 0.0's used for the centroid with the gaussian quadrature values for all 8 nodes, then report the minimum (too tedious for hand calculation!).

I'll only mildly apologize for the large size and ugly figures, since it's free. Hope this is useful!

Albert

A typical term in a finite element equation resembles:

Although we don't know eta(x), we do know x(eta):

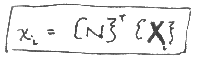
where {Xi} is the nodal coordinates of the element

So, the inverse:

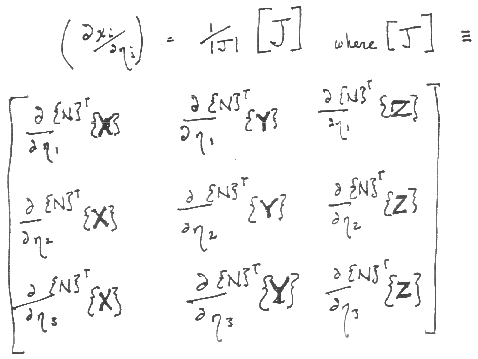
is "easy" to evaluate.

EXAMPLE:,

For a trilinear hexahedron defined as:


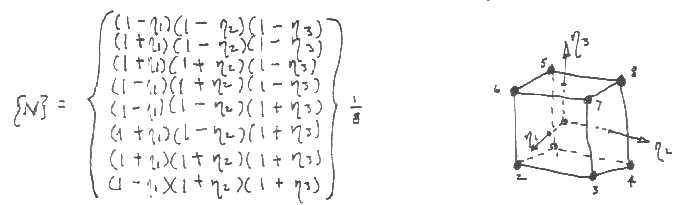
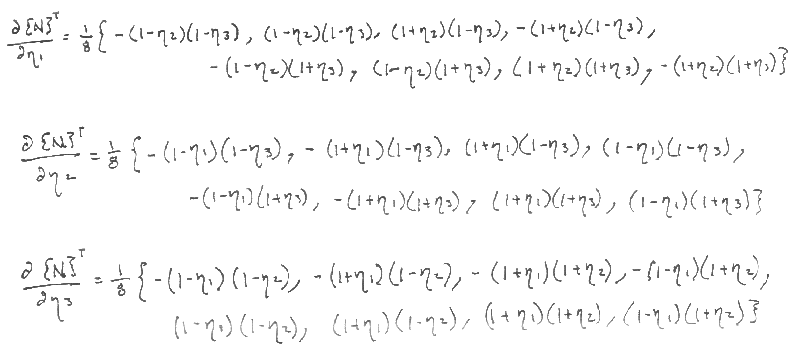
Evaluating at the CENTROID (not at the Gauss points!!),

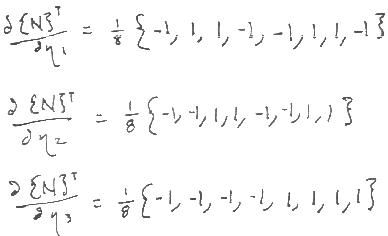
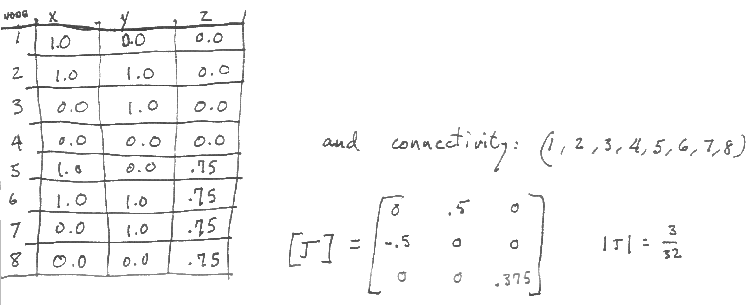
For an element defined with nodal coordinates:

where all matrix entries are zero except:

EXAMPLE 2

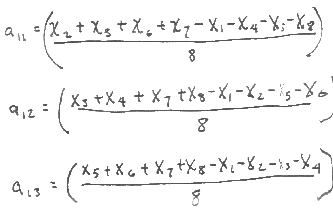
For a 6-noded pentahedron (wedge):

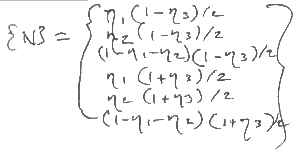
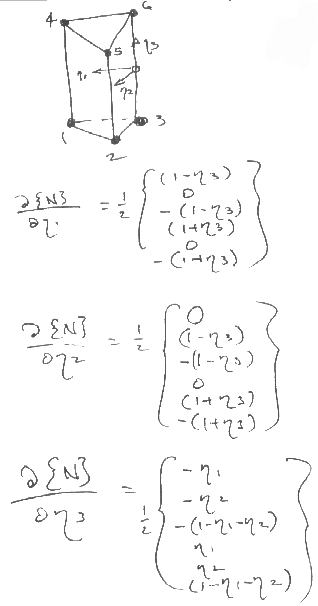
so the centroid is again used to evaluate the eta's instead of the gauss point




EXAMPLE 3

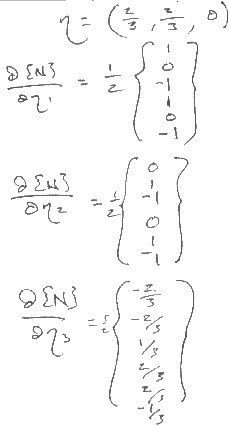
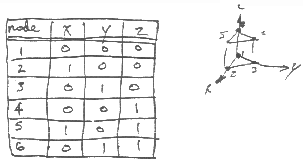
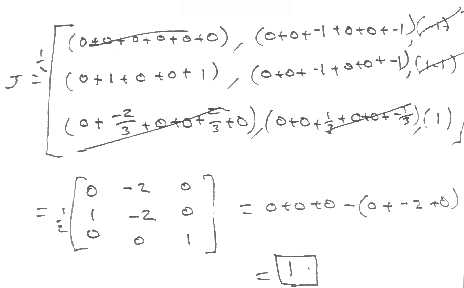
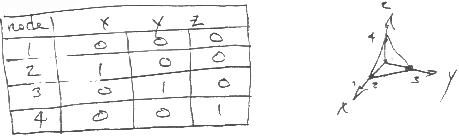
For a 4 noded tetrahedron:



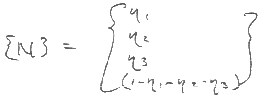
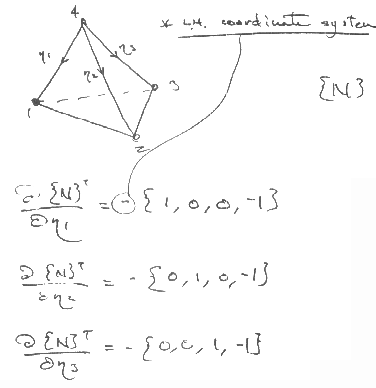
So, since a purely linear element has constant derivatives, the true jacobian is worthless for 4-node tetrahedra. Hence it is common to replace it with a volumic measure, to remain consistent with the other element's jacobians.

EXAMPLE: